The open loop transfer function of a unity gain negative feedback system is given as $$G \left ( s \right ) = \dfrac{1}{s\left ( s+1 \right )}$$
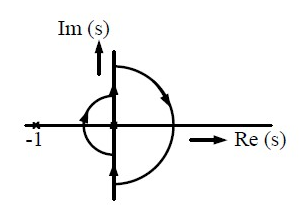
The Nyquist contour in the $s$ -plane encloses the entire right half plane and a small neighbourhood around the origin in the left half plane, as shown in the figure below. The number of encirclements of the point $(-1 + j0)$ by the Nyquist plot of $G(s)$, corresponding to the Nyquist contour, is denoted as $N$. Then $N$ equals to
- $0$
- $1$
- $2$
- $3$