An $\text{LTI}$ system is shown in the figure where $$G \left ( s \right ) = \dfrac{100}{s^{2}+0.1s+100}$$ The steady state output of the system, to the input $r(t)$, is given as $$y \left ( t \right ) = a +b\:\sin\left ( 10t + \theta \right )$$ The values of $’a’$ and $’b’$ will be
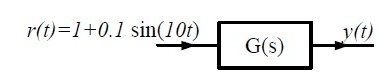
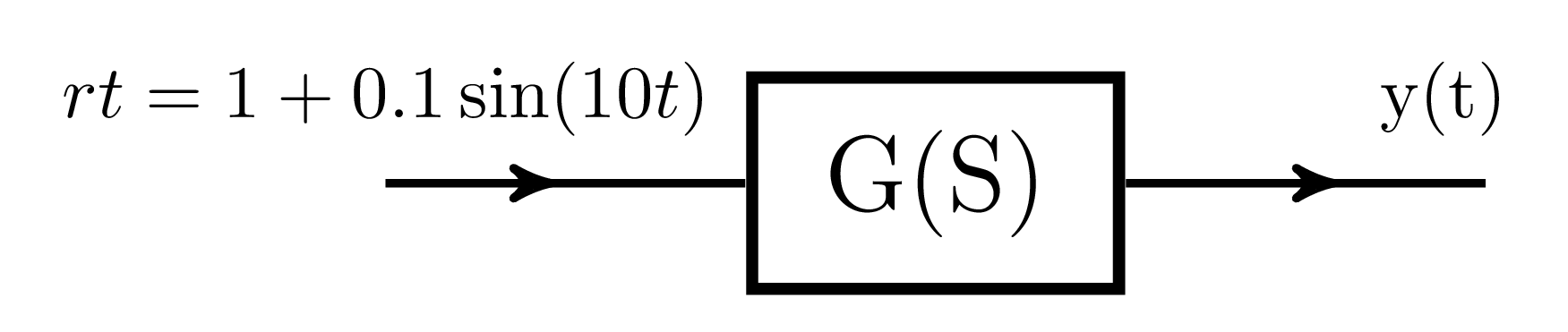
- $a = 1, b=10$
- $a = 10, b=1$
- $a = 1, b=100$
- $a = 100, b=1$