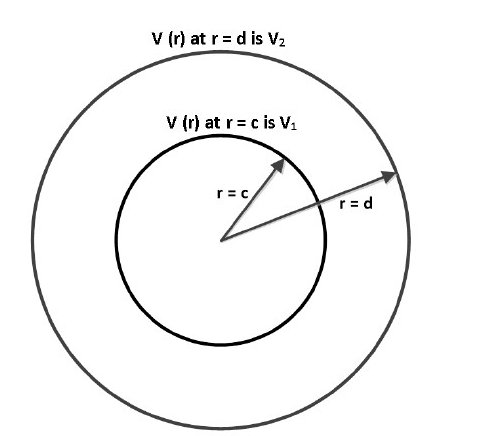
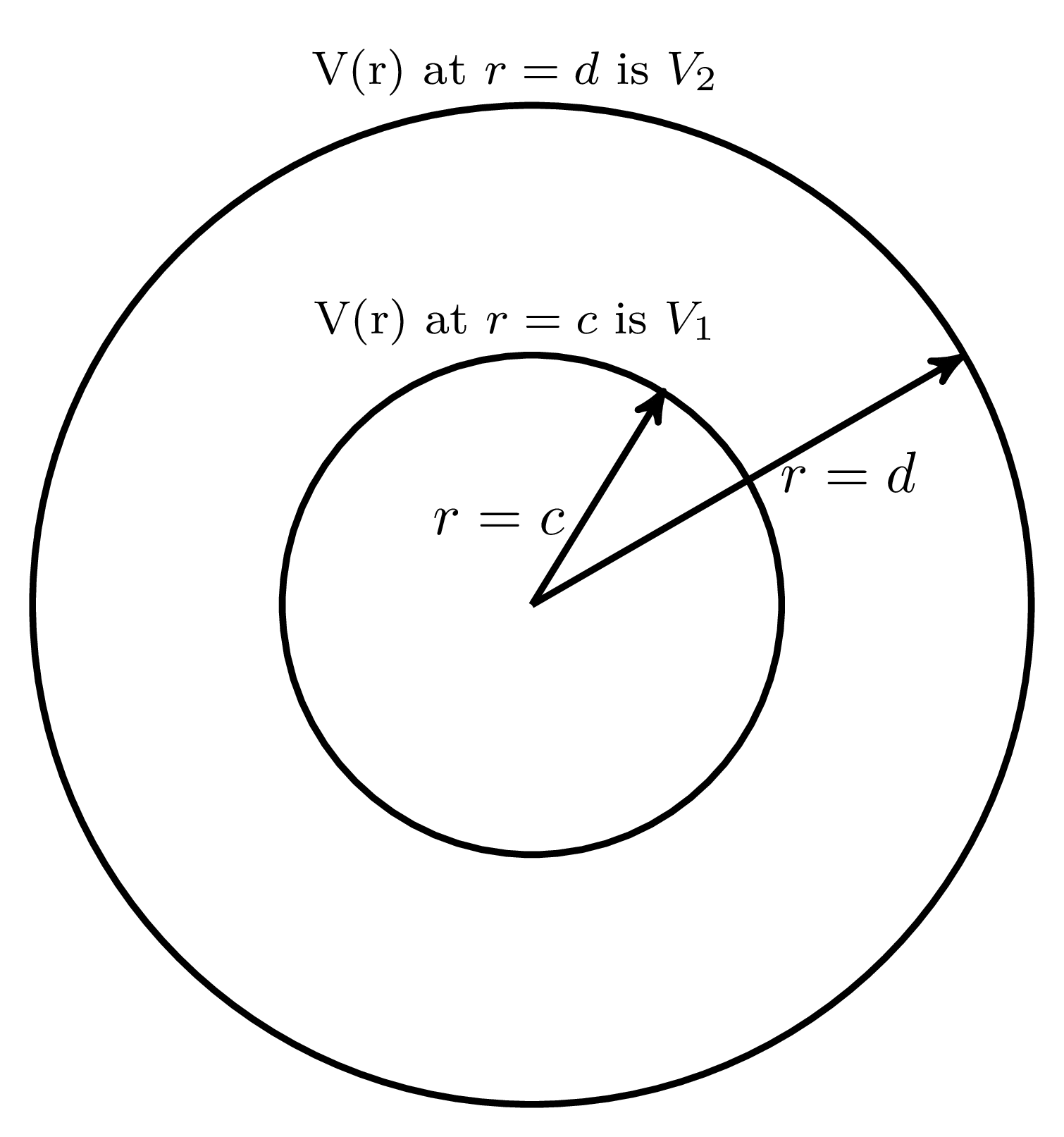
As shown in the figure below, two concentric conducting spherical shells, centered at $r = 0$ and having radii $r = c$ and $r = d$ are maintained at potentials such that the potential $\text{V(r)}$ at $r = c$ is $V_{1}$ and $\text{V(r)}$ at $r = d$ is $V_{2}$. Assume that $\text{V(r)}$ depends only on $r$, where $r$ is the radial distance, The expression for $\text{V(r)}$ in the region between $r = c$ and $r = d$ is
- $V\left ( r \right ) = \dfrac{cd \left ( V_{2} - V_{1} \right )}{\left ( d -c \right )r} - \dfrac{V_{1}c + V_{2}d - 2 V_{1} d}{d -c}$
- $V\left ( r \right ) = \dfrac{cd \left ( V_{1} - V_{2} \right )}{\left ( d -c \right )r} + \dfrac{ V_{2}d - V_{1} c}{d -c}$
- $V\left ( r \right ) = \dfrac{cd \left ( V_{1} - V_{2} \right )}{\left ( d -c \right )r} - \dfrac{ V_{1}c - V_{2} c}{d -c}$
- $V\left ( r \right ) = \dfrac{cd \left ( V_{2} - V_{1} \right )}{\left ( d -c \right )r} - \dfrac{ V_{2}c - V_{1} c}{d -c}$