The magnitude of magnetic flux density ($\vec{B}$ ) at a point having normal distance $d$ meters from an infinitely extended wire carrying current of $I$ $A$ is $\dfrac{\mu i}{2\pi d}$ (in $SI$ units) (in SI units). An infinitely extended wire is laid along the $x$-axis and is carrying current of $4$ $A$ in the $+ve$ $x$ direction. Another infinitely extended wire is laid along the $y$-axis and is carrying $2$ $A$ current in the $+ve$ $y$ direction. $\mu_0$ is permeability of free space. Assume $\hat{i},\hat{j}$ and $\hat{k}$ to be unit vectors along $x$, $y$ and $z$ axes respectively.
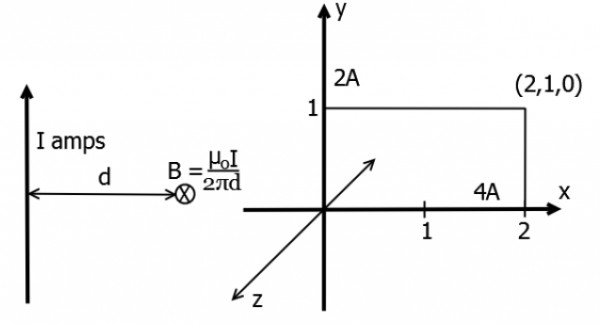
Assuming right handed coordinate system, magnetic field intensity, $\vec{H}$ at coordinate $(2,1,0)$ will be
- $\dfrac{3}{2\pi }\hat{k} \text{ weber}/m^2 \\$
- $\dfrac{4}{3\pi }\hat{i} \: A/m \\$
- $\dfrac{3}{2\pi }\hat{k} \: A/m \\$
- $0 \: A/m$