Let $x_{1}(t)\leftrightarrow X_{1}(\omega )$ and $x_{2}(t)\leftrightarrow X_{2}(\omega )$ be two signals whose Fourier Transforms are as shown in the figure below. In the figure, $h(t)=e^{-2|t|}$ denotes the impulse response.
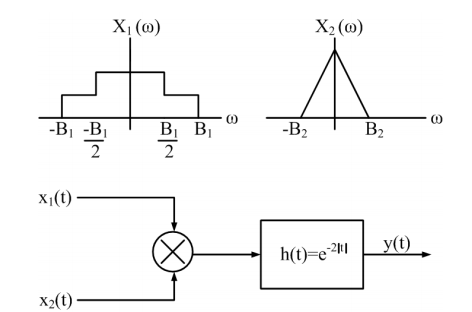
For the system shown above, the minimum sampling rate required to sample $y(t)$, so that $y(t)$ can be uniquely reconstructed from its samples, is
- $2B_{1}$
- $2(B_{1}+B_{2})$
- $4(B_{1}+B_{2})$
- $\infty$